A fundamental question in fluid dynamics: vorticity generation
Is vorticity generation at surfaces a viscous mechanism? This is one of the fundamental questions in fluid mechanics, and it has a big impact on how fluid dynamics (FD) and aerodynamics are understood today. I posted such a question a few days ago in a LinkedIn group called "Computational Fluid Dynamics" with about 28K members. Surprisingly, it has been replied to by 34 people so far (about 0.12%), which is actually more than expected, considering that most of the publications there do not get a single "click" (most of them for "likes"). Do not be cruel, click on them!
Fig. 1 Results for the question after 34 votes (there were 35, but someone removed his participation).
I suspect that this "huge result" is due to the controversial nature of the question, which has been simplified to reach a wider audience. According to public information, the participants come from universities to research centers, including both industrial and academic profiles. However, as in most democracies, every vote has the same value, regardless of their level of knowledge or experience on the subject. In the end, most members of the group should be able to understand the meaning of the words "vorticity," "surface," and "viscosity," at least in a vague way. This will also help us to get a big panorama, which is the main goal of such a publication. By the way, thanks in advance to all participants; in the end, the only thing that counts is the effort to find the right answer (if we can!), nothing else. A special mention should be given to some who chose the last option in the survey ("Who cares, I just push buttons"). First of all, they certainly have a sense of humor 😁 or maybe they just want to be ironic like I tried to be, anyway...In my opinion, a sense of humor (but not all the kinds) is one of the most important things in life, even more than knowledge!
Although such a test was accompanied by a short explanation of my perspective for answering this question, based on my research, which includes three peer-reviewed journal articles and an international patent application (which meets all preliminary requirements for patentability, according to the corresponding authority), the intention was not to change anyone's mind. In the end, such a format is not optimal for discussing such topics, but only to refer to my latest scientific publication [1], which could help to strengthen my point of view, which according to this test is opposite to the most voted option.
Trying to answer a question with another question does not seem to be the best strategy to get an acceptable answer in any sense, but it can be useful to try to explain our perspective and to put the question up for debate, if not openly, at least as an idea to consider for future argumentation. One such additional question concerns the explanation of how vorticity can be generated on a solid surface in a non-viscous fluid. Such an explanation is oversimplified, but in the end, it might help to show the justification behind at least one of the existing theories mentioned in the original post (The generation and decay of vorticity; B.R. Morton, 1984).
Q: But how can such an inviscid phenomenon be physically understood?
A: Since at the molecular level fluid particles cannot be represented by perfect spheres but by irregular shapes (even aligned with the free stream), they change their angular momentum (ideally from zero to some value) during their "contact" with a solid boundary (even if this is perfectly smooth), thus creating a tendency for rotation or vorticity (remember that 'inviscidity' is assumed only for the flow, not between it and surface particles at the solid-fluid interface). Hence, vorticity generation is reduced to a purely mechanical phenomenon! Then such molecular-sized "eddies" interact (collide) between them to form more complex vortex structures.
Fig. 2 Hypothetical inviscid fluid (blue-purple shapes) near a perfectly smooth solid surface (black line). 'Inviscidity' is assumed only for the flow, but not for the entire fluid-solid domain.
If, after reading this, you think that this explanation is too simple and you want to make it more complicated, consider that a Lagrangian approach can explain the behavior of detached fluid particles by a "small balls-and-sticks" scheme [1]. In the end, CFD is simpler than some people want to make it seem; the complexity is in the methods chosen (for meshing and approximating the solution), but not in its nature (it is quite similar to solid mechanics!*), at least not for the incompressible case.
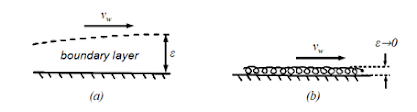
Paradoxically, the most popular answer so far ("yes": viscosity is required for vorticity generation at surfaces) is consistent with the current interpretation of Potential Flow Theory (PFT), which models laminar (a supposedly vorticity-free field; in fact, vorticity is concentrated in an infinitesimally thin boundary layer; see Fig. 3) flow patterns around general geometries, avoiding any flow separation and thus giving unphysical results, especially for bluff body configurations in the upper Reynolds number limit (Re→∞), where such a theory is theoretically established. This is probably the reason why the PFT is no longer well accepted (or unknown!) by most fluid dynamists (or maybe it is, according to the present test results!), since it does not solve correctly for flow separation cases. As an alternative, solutions based on the Navier-Stokes equations (mostly in their Eulerian description) have become the standard in the last decades to approximate the fluid-flow behavior around objects and more complex phenomena.
Fig. 3 (a) Finite Reynolds number case: boundary layer development; (b) Infinite Reynolds number case: boundary layer of infinitesimal thickness (concentrated vorticity).
But what are my intentions? do I want to discredit or destroy the PFT? Absolutely NOT!!! on the contrary (my research is based on such a theory!), although some hardcover book potentialists have been offended (calling my research "illogical", "theoretically unjustifiable" or "unphysical"). Well, maybe they don't like the way I say things, but...I really can't understand how they can defend tooth and nail an interpretation of a theory from more than two and a half centuries ago that has only been proven to be valid for certain specific operating conditions (thin bodies at the low angle of attack range), mainly in low-fidelity computational aerodynamics. Reduced computational times cannot be a sufficient justification for making assumptions and generalizations (or even worse, apply "corrections" to match the expected results!); we must first understand the phenomenon, then construct a general model, and only then apply well-justified simplifications. Now that I have the results, it is time for my detractors to have proof to the contrary. Fortunately, Science is not about what we want to believe, but about what we can prove.
*a solid can be treated as a very-high-viscosity fluid (see "pitch drop experiments").
“You do not really understand something unless you can explain it to your grandmother.” —A. Einstein or R. Feynman or someone smart.
Q1 journal article: The Full Non-linear Vortex Tube-Vorton Method: the pre-stall condition | Advances in Aerodynamics | Full Text (springeropen.com)
Something interesting to watch:
Video: A 25 min. presentation: Detached potential flow and vortex methods (Pimentel, 2024).




Hi, I'm not really sure what the example with the fluid "molecules" is meant to explain. It feels like a 17th-century approach to fluid dynamics, but not even a consistent one: for example, why the interactions with the wall are considered a viscous phenomenon, but the interactions between the fluid "molecules" are not?
ReplyDeleteI have read the paper you cited, but it describes a computational method, there is no mention of anything concerning viscosity, or vorticity generation.
Hi CT,
DeleteIn such an example, I'm not trying to describe a viscous phenomenon, but a purely inviscid one, where fluid particles are freely detached from the surface (with vorticity after collision) precisely because of the lack of viscosity in the fluid (explained as the degree of aglomeration of fluid particles on surfaces and their resistance to flow). Note that in a hypothetical inviscid fluid such aglomeration is reduced to a minimum. We must remember that, of course, the presence of viscosity inhibits (diffuses) vorticity, not the other way around. When I say that the flow-solid interface should not be considered inviscid, it is because when we say "inviscid fluid" we are referring only to the flow domain, not to the entire domain (fluid-solid domain); solids are not inviscid flows, in fact they can be considered very high-viscosity fluids. From this point of view, the interface has no viscous or inviscid attribute, so the flow behavior is determined only by what happens in the fluid domain (isolated by a wall) and its physical properties.
Thanks for reading the paper. Yes, you are right, it describes a computational method (based on a series of two previous articles) that tries to explain an extremely simple hypothesis: if viscosity allows fluids to adhere to surfaces, inviscidity allows them to detach. Sounds logical, right? From the beginning, my research has been based on a purely numerical approach to avoid dealing with assumptions, beliefs and unjustified simplifications; now I am trying to explain the phenomenon of detached flow according to such results. I invite you to read more short articles in this blog to get a broader panorama of this research.
Thanks in advance.
Thanks for your answer. My point was, why do you call "viscous" the collision with the wall, but "inviscid" the collision between the fluid particles? And how the mechanism you describe in the example is different from the interpretation of viscosity as "friction", i.e. forces between molecules (mechanical, or electromagnetic, which is more realistic)?
DeleteBy reading some of the other posts I seem to understand that your plan is to include flow separation as part of PFT, am I correct? This would be fine, as long as it gave an useful model. Is it possible to predict separation according to your interpretation?
Hi back CT,
DeleteNo, from my perspective, the whole process (generation of vorticity) is inviscid, as I tried to explain. The viscous effect you are referring to is within the PFT. According to (G. Batchelor, "An Introduction to Fluid Dynamics", 1967; p. 79): "Theoretical results concerning the flow of an inviscid fluid may thus be applied directly to the former class of cases in which boundary-layer separation does not occur; here inviscid-fluid theory provides us with a good approximation to the flow of a REAL fluid at LARGE Reynolds number (with the same initial and boundary conditions) over the whole region of fluid, EXCEPT in thin layers whose thickness approaches ZERO as ρLU⁄μ→∞ and whose position is known from the inviscid-fluid solution". Thus, a well-known viscous property (flow attached to surfaces) is arbitrarily imposed by the current PFT. A true inviscid flow must allow vorticity to detach from the entire surface. I prefer not to speculate about other physical forces that might be involved; from my current point of view and understanding, vorticity generation is a purely mechanical process (however, aglomeration of particles could explain viscosity near the solid wall).
Yes, you are right. I have developed a numerical method to accurately account for fluid-flow separation behind plates under both PFT and vortex method approaches. The main advantage of the latter is that it avoids the use of turbulence models (as Eulerian methods do) to predict flow separation, which was naturally achieved in the 2D case. Its extension to the 3D case must be straightforward since the principles and concepts are practically the same, which has been successfully applied in the bidimensional case.
Thanks for your interest.
My point was that the mechanical action that you introduced in your "molecular" example can simply be called viscosity. Viscosity is nothing but a component of stress. Without this component, fluid can slide past bodies and other fluid portions. The exerpt from Batchelor is only saying that real viscous flow also seems to slide past, i.e. the external flow slides past the boundary layer. The reference to LARGE Reynolds is there only to imply that boundary layers are small, so that the external flow represents almost the entire flow region.
DeleteIn your method, how do you predict separation? It seemed to me that the answer is "it is already separated", but that's hardly a prediction.
Also, how do you explain that only the suction side of an airfoil/plate presents separated flow?
I apologise for all the questions, but I have to be convinced of a new idea or method before committing myself to it.
No problem, it is good to take the time to develop the ideas better.
DeleteIn vortex methods, separation is naturally achieved since it depends only on the velocity field, which could include vorticity diffusion in a viscous fluid. In the case of unsteady LAR plates presented in my last paper (The Full Non-linear...), the flow seems to be attached to the surface, but not due to viscosity, but due to the total induced velocity field; in high Re aerodynamics, the small viscosity is not a sufficient reason to keep the fluid attached to the surface.
On the suction side, flow separation in a plate is most likely due to the sharp (zero curvature) leading edge. In the case of an airfoil, it is due to curvatures (change in direction to the flow). To generalize, flow separation depends on the ratio of inertial and viscous 'forces' (Re) rather than shapes or fluid viscosity per se. I tried to explain it better in a blog article related to Coanda effect. In pressure side (lower part) of an airfoil or plate at AoA, avoiding of separation (in a strict sense, it should exist in an inviscid flow) it obbeys more to a geometrical aspect (inclination angle respect to the flow).
If flow separation depends on viscous forces, then viscosity does affect separation? I thought it shouldn't, based on your interpretation.
DeleteI am trying to understand the advantages of your model, but so far it seems to me that it assumes separation just as all the other mid-fidelity methods do (eg by imposing wake release at the trailing edge), without specific criteria or descriptions of where and why separation occurs.
In such a blog article, I concluded there that separation depends on the ratio of inertial and viscous forces (Re), but not only on the shape of the body or the viscosity value itself. IMO, it makes absolutely no sense that fluid separation is provoked by fluid viscosity existence; by definition, viscosity is a property that keeps fluids attached to surfaces, not the other way around.
DeleteIf one assumes an inviscid flow, no specific criteria or descriptions are necessary for such a calculation, the flow must separate everywhere. Fluid dynamics is only one, and it should work the same under all conditions without any additional assumptions or simplifications. The Lagrangian formulation of the NSE allows to solve a dynamical problem by a dynamical approach.
Viscosity is a friction effect, not an attraction effect (at the macroscopic level): it does not keep fluids attached to solid surfaces, it prevents fluids from sliding freely on them, which is not the same thing.
DeleteNotice that separation in inviscid flow was already included in the "free streamline theory" by Helmholtz, which includes a "dead water" region where the flow is separated: the latter, however, was taken as an hypothesis, and still the recirculating flow was too important for the theory to correctly predict drag.
I think a criterion for flow separation is necessary. How can I predict that an airfoil at incidence separates, say, at 80% chord instead of at 60%? If everywhere is separated, what does "separation" actually mean for you? Is flow recirculating with eddies everywhere around a body? I surely have never seen that.
Fluid dynamics *is* only one, but in all of science assumptions and model are chosen to simplify the problem and make it tractable. You can take the most general equations for relativistic magnetohydrodynamics of fluids of the second order, but hardly anything would come out of them. That's why, for example, we ignore compressibility when it's not important; but if I were to apply Prandtl-Glauert corrections to the results of an incompressible simulation (or, a better analogy, if I were to hypothesize the position of shockwaves), I wouldn't then claim that actually compressible effects can be explained without thermodynamics by an incompressible theory.
In the 2D case, the Kirchhoff-Rayleigh inviscid separated (perpendicular to the plate) flow shows an underestimated drag coefficient. According to (Batchelor, 1967; sub-chapter 6.13 Free-streamline theory, and steady jets and cavities), it solves a "cavity flow" with vacuum behind the plate, or in other words, no vorticity is modeled directly behind the plate; thus, by analogy to 3D, it would also model a cavity case. I just copy and paste a paragraph from my first paper in the series (The Full Multi-wake VLM:...).
DeleteAs I just said, in vortex methods, separation depends on the flow solution (i.e., velocity field) and the degree of attachment/detachment is not assumed or modeled a priori; a viscous model (which inherently modifies the velocity field due to diffusion of vorticity) does that. This animation (not mine) shows eddies everywhere (even before deploying the spoiler) for a "laminar" fluid condition:
https://www.youtube.com/watch?v=H-snLmMQK0Y
We both understand that this problem is limited to the incompressible case. So, under such a limitation, I am talking about a "generalization" within such a restriction.