Fluid dynamics for dummies, like me: on potential flows

Potential Flow Theory (PFT) has always had a bad reputation among most fluidynamicist, among other things, because it is quite abstract and has only been successfully applied to explain, more or less, basic concepts of fluid dynamics, more specifically in aerodynamics, mainly through low-order numerical methods, such as panel ones, including the "well-known" vortex lattice method (VLM).

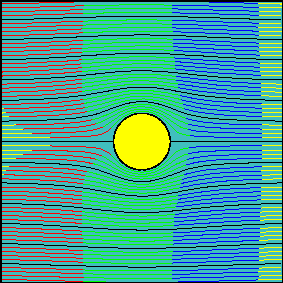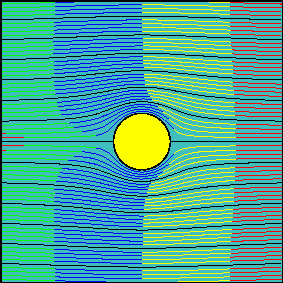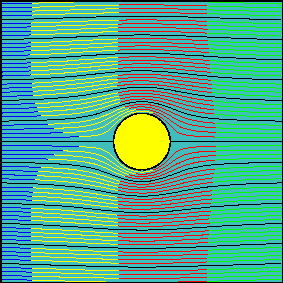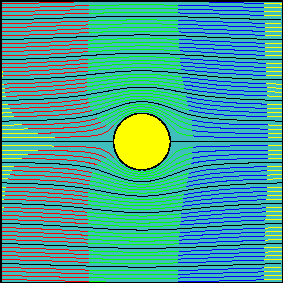
Most lecturers teach during the fluid dynamics or computational aerodynamics courses that the PFT defines an irrotational (vorticity-free), incompressible (divergence-free) and inviscid (viscous-free) flow, which they call "ideal". However, its supposed inviscid characteristic is not theoretically defined and its current numerical implementation (including its attached circulation) is only a crude assumption! Such a misunderstanding can be demonstrated with a single image, from which it can be concluded that in fact, the current interpretation of the PFT has been used until now to solve its counterpart—I mean, the viscous case!!!, A BIG, A BIGGER, THE BIGGEST mistake in its interpretation that has been present since its conception around three centuries ago and has caused a serious delay in the development of Lagrangian vorticity-based methods, the most natural way to solve fluid dynamics!

The best-known example of the inconvenience caused by the current interpretation of the PFT is related to d'Alembert's "paradox", which in fact results in a fallacy. According to such a theory, it is not possible to obtain any force, including drag, in an "inviscid" flow past a cylinder, which is opposite to what is naturally expected. According to experience, an immersed object that moves inside a fluid exerts a drag force in the opposite direction to its path. But wait! Before you try to justify it due to the lack of fluid viscosity, please carefully take a look at the next image:

Fig. 1 Water flowing past a circular cylinder at an extremely low Reynolds number. 
Source: https://dlatreyte.github.io/terminales-pc/chap-20/chap-20-2/chap-20-2-dynamique-fluides-6.png

The previous picture is retrieved from page 8 of 'An Album of Fluid Motion'  (1982) by Prof. Milton Van Dyke from Stanford University, and it corresponds to a Hele-Shaw or Stokes 'flow' (in fact, fluid, because it is water, not a superfluid!) past a circular cylinder (between two glass plates) flowing at 1 mm per second (an extremely low velocity!). Aha, and then?! Well, do you remember the definition of the Reynolds number (Re)? Yes, it is the ratio between inertial (due to its movement) and viscous (due to its stickiness) forces, right? 


If the fluid velocity is extremely low as in this case, the viscous effect dominates and the Reynolds number tends to zero (Re<<1). Even so, the author points out: 'It is a first-sight paradoxical that the best way of producing the unseparated pattern of plane potential flow past a bluff object, which would be spoiled by separation in a real fluid of even the slightest viscosity, is to go to the opposite extreme of creeping flow in a narrow gap, which is dominated by viscous forces'.

So, according to this experiment, it is obtaining 'almost' a fully viscous streamline pattern (a fully viscous one must represent stagnant flow without any streamline), which is the same (or almost) as that obtained through the "ideal" ("inviscid") flow defined by PFT through the stream function! (see the next animation):

Fig. 2 Potential Flow Theory simulation for an 'ideal' flow past a circular cylinder. 
Source: https://www.av8n.com/irro/animation/cilsmo000.gif

According to the definition of the Reynolds number, for an inviscid flow (or viscous forces equal to zero), such a Reynolds number takes an infinite value in the theoretical case! (do not forget division by zero from highschool mathematics), while in the experiment such a Reynolds number tends (not exactly but closer) to zero! A complete inconsistency between both results, considering that both of them are focusing on show the same phenomenon!
 
At this point, there is only one correct option. I have chosen mine; now choose yours:
a) The physics are wrong! πŸ˜†
b) The experiment is wrong! 😟
c) The theory is wrong! 😒
d) The current interpretation of the theory is wrong! 😎

Possible answers:
a) Probably not, at least not in this universe.
b) It is a possibility, but more related experiments appear in the same book with a similar pattern (see fig. 6 at Re=0.16)...
c) If it is true, then we are worse than in the beginning. It's better not to think about it!
d) According to the most simple logic (and convenience), this seems to be the correct answer. πŸ‘ˆ

By the way, why do a potential flow method's (panel, vortex lattice or lifting line) results often match total CL (in the linear region; low AoA range), which is supposed to be viscous, the same as (viscous) RANS and experimental ones? In other words, why is an inviscid method capable of obtaining viscous results directly (without BL coupling)? Does it mean that lift 'force' generation is a purely inviscid mechanism? Where has the viscosity gone?



Fig. 3 Lift coefficient vs angle of attack for a complete UAV configuration obtained by viscous and inviscid computational methods. Source: [1]

And with all this, what is the use of knowing? Well, check it out for yourself! (Click on each one):

Comments

  1. AnonymousOctober 2, 2023 at 4:15 AM

    Hi Carlos, it is difficult to see what you're trying to argue here. The similarity between the flowfield images would break down simply by zooming in and finding the boundary layer. The main difference between a flow of a viscous fluid and of a perfect fluid is the boundary condition of adherence vs. non-penetration, respectively.
    Also how is the Euler-D'Alembert paradox a fallacy? I've read your post on the matter, but it wasn't really clear to me.

    ReplyDelete
    Replies
    1. Carlos PimentelOctober 2, 2023 at 2:13 PM

      Hi! Perhaps what needs to be clarified is that I am referring to the macro scenario, not the micro one. Please give me some time to prepare a better explanation. Meanwhile, keep in mind the next four scenarios:

      1) Physical/hypothetical: the fluid-flow is totally viscous (Re=0), then there is no velocity (completely stagnant flow), no BL and no streamlines are present; the drag force is zero.

      2) Physical; Stokes 'flow': the fluid-flow velocity is near (q-->0) to zero (Re-->0), thus, it cannot be already completely viscous (nu-->inf); the BL is just developed; it has an 'almost' infinitesimal thickness, despite the high viscosity, due to the low velocity (low shear stresses); drag force just appears (D-->0).

      3) Current PFT: the flow is supposed to be completely inviscid (Re-->inf), thus no shear stresses despite the high velocity (or a large characteristic length). If it is supposed that BL cannot exist due to the inviscid condition*, no interaction with the surface is possible, and no drag force can be obtained. This solution is trivial since no matter the body's shape/streamline pattern, the result will always be the same.

      4) New interpretation of the PFT: Since the flow is entirely attached to the surface, the fluid-flow is 'almost' completely viscous (Re-->0). The BL is confined to an infinitesimal thickness (it cannot grow due to the low fluid-flow velocity). This explanation matches the second scenario, the physical one.

      *This is false because it can be theoretically demonstrated that vorticity (thus, circulation necessarily exists) can be generated from surfaces without a viscous medium, being a purely inviscid mechanism [Terrington et al., 2022].

      I just answered the other question in the corresponding post.

      Thanks for your interest!

      Delete
    2. AnonymousOctober 4, 2023 at 4:17 AM

      First of all, thank you for your sharing your thoughts, which gave me the opportunity to do some very interesting reading.

      I am looking forward to a more detailed post, and I would like to add here some considerations:
      1) Everyone agrees that PFT is very useful for a "macro" description of flows
      2) That the potential flow solution closely resembles the low Re flows and not the high Re ones has more to do with instability than with viscosity per se
      3) in general, flows of inviscid and viscous fluids are qualitatively different, and the difference is big enough that Re has no meaning for inviscid fluids, not even as a limit.
      4) the difference lies in the boundary conditions you impose, adherence vs non-penetration; on this, the work by Terrington and the related ones show that yes, viscosity does not generate vorticity, but the adherence condition is always imposed, which has a meaning only for viscous fluids.
      5) irrotational viscous flow can exist, but only in some special cases where it manages to satisfy adherence.


      Delete
    3. Carlos PimentelOctober 6, 2023 at 12:27 PM

      Thank you for reading my blog and having a genuine interest in these topics. Now, I will write a brief discussion of your points with the intention of continuing to generate ideas, which in the end is what really matters.

      1) Yes, through the current accepted interpretation of PFT.
      2) I am not sure about this, but in the end the PFT allows obtaining good agreement through potential methods (at least for lift force in the viscous range without any BL coupling) for simulations that operate in high Re (e.g., airfoils, wings or airplanes).
      3) In the limit, a flow is a fluid without viscosity or even with a slight one (e.g., nu=0.000...001 and this continues to be a fluid despite the extremely low viscosity), and then you can use the Re definition. What I want to show here is that if we have some problems understanding a phenomenon exactly at its extreme points, we can always use limits. This way of thinking is more useful than it appears. I often use it!
      4) From the current interpretation of PFT, the imposing of a non-penetration (zero normal velocity, thus tangential flow) BC is not related to an inviscid or viscous attribution of the flow but only to restrict its crossing/penetrating through the surface; I mean, a no-slip (adherence) of even free-slip BCs is not imposed explicitly in PFT; in any case, only the second one is imposed implicitly (from the current interpretation).
      5) It can exist, but not in the scope of PFT but in the Navier-Stokes one, for example, through vortex methods.

      By the way, I just published a new post (A four-question...) where I try to simplify my reasoning from an observational point of view. I also recommend the reference to the Coanda effect, in order to expand this order of ideas.

      Delete
    4. AnonymousOctober 9, 2023 at 8:43 AM

      I have replied to some of those points in the comments of your newest post.
      3,4,5) About the boundary conditions, adherence is not imposed in PFT because it would over-constrain the equations and make irrotational motions (almost) impossible. It is imposed for (linearly) viscous fluids, making the problem well-posed, in accordance to experience; I'm setting aside particular flows (rarefied gas, non-linear viscous fluids) for which different boundary conditions should be imposed. So it's not a matter of "extreme points", it's two totally different approaches, especially from a mathematical point of view.
      The behaviour of ideal fluids might be difficult to understand, but that's because we never see ideal fluids (at least in our daily life).

      Delete
    5. Carlos PimentelOctober 9, 2023 at 6:44 PM

      Thanks for maintaining the interest. I will try to answer there.

      Delete

Post a Comment

Popular posts from this blog

On detached potential flow and the d'Alembert's paradox (September-2022)

Image
The Potential Flow Theory (PFT) states that a 'potential flow' must be incompressible (divergence-free) and irrotational (vorticity-free). However, compressible potential flow also exists, but it is not defined within the classical PFT. Then, strictly and in a broader sense, a potential flow must only fulfill the irrotationality condition. At this point, the term 'viscosity' is absent from such a definition, however, for the same reason that such a term does not appear, the fluid-flow viscosity value can be considered zero. Then, an 'inviscid potential flow' is now called an 'ideal flow' in order to be more specific. However, from the current interpretation, a viscous-forced potential flow (Kutta-Zhukovski-type pseudo- real flow) can also be defined, hence, 'potential flow' is not a synonym of ideal flow, as most authors misunderstand. In other words, the ideal flow is a potential flow, but a potential flow is not necessarily the ideal flow
Read more

Could there be lift without viscosity?

Image
One of the classic debates in aerodynamics (or fluid dynamics, in general) is whether the existence of viscosity in a fluid is an essential condition for the generation of lift 'force' in an immersed body. First, the concept of viscosity must be explained, which is a property that is closely related to the physical constitution of the fluid at a microlevel, that is, at the molecular scale. Thus, this can be understood as the level of resistance or friction that its "particles" oppose to the displacement of their neighbors in the tangential direction (with respect to the flow), and that depends on the time it takes for the particles of an 'upper layer' to fill the spaces left in a 'bottom layer' (relative to a 'solid wall') as the fluid flows. Fig. 1 CASA-295 aircraft CFD simulation (just to get your attention!). To put it in context, a typical example of a fluid with a high viscosity is honey, which moves more slowly than water, which has a muc
Read more