Does the Coandă effect "cause" lift on an airfoil?
Since the Coandă effect (CE) is precisely an 'effect', it cannot be by itself a cause of any force, the same as the pressure field in the velocity-vorticity formulation of the Navier-Stokes equations (vortex methods), in which such a field is decoupled from the flow solution (it can be obtained by reconstruction of the stream function). The real cause of lift (and drag!) generation is vorticity, detached from the entire surface [1,2,3], in addition to viscosity (under certain operating conditions; low AoA range). Thus, the correct question should be: Is the "Coanda effect"* related to lift on an airfoil? The short answer is: yes, and no. I mean, in first instance, it depends on the orientation of the flow when such an airfoil is operating. For the low AoA range, the CE seems to be present due to the effect of the viscosity and the curvature in contact with the fluid; however, if such an airfoil (at the same Reynolds number; Re) is stalled, the CE is absent since the flow is fully detached from the leading edge; however, lift is still being generated. The next picture helps to visualize the previous idea:
Fig. 1 Fluid flow past an airfoil at different angles of attack. Source: https://1.bp.blogspot.com...
At this point, it is clear that for a flat plate with a near-zero curvature radius (or sharp) at the leading edge, the CE practically does not exist under 'normal' values of viscosity. Experimental results for a quadrangular flat plate show that the linear viscous range, where the CE is supposed to be completely present, is reduced up to 2 degrees of AoA; ideally, for an infinitesimally thin flat plate in an inviscid flow, it should be zero!
As said before, since the CE is an 'effect' and not a 'cause' as its name suggest, its cause is partially viscous, as was explained before; however, does it explain the curvature of the streamlines behind a circular cylinder from the current interpretation of the Potential Flow Theory (PFT; see the next animation)? Let's see.
Fig. 2 Potential flow past a circular cylinder. Source: https://www.av8n.com/irro/animation/cilsmo000.gif
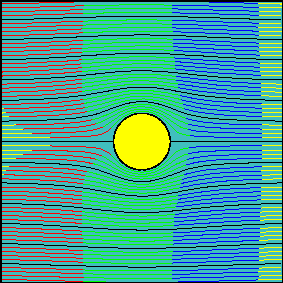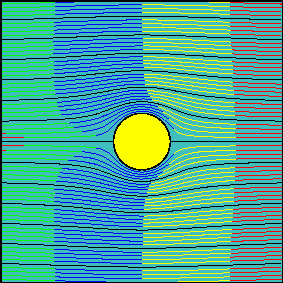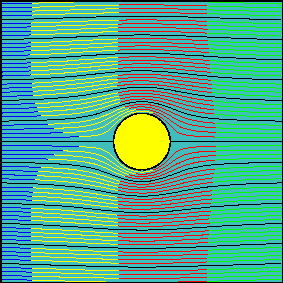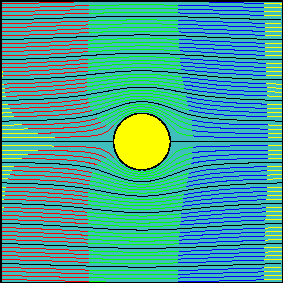
The ideal flow is defined as irrotational, incompressible and inviscid by the current interpretation of the PFT. In consequence, if the CE is inherently supposed to be viscous and the ideal flow is inviscid by definition, the curvature of the streamlines cannot be justified by such an effect, but in any case, only by the surface curvature. It should be remembered that, since there is no viscosity in an ideal flow, the relation between inertial and viscous effects (or Re) tends to be infinite (division by zero). But, what happens in the opposite situation? Where the viscous effects dominate over the inertial ones, or, in other words, the Re tends to zero. Well, in this case, the CE completely justifies the streamline pattern observed in experiments (see the next picture: water flowing at Re<<1):
Fig. 3 A viscous fluid past a circular cylinder at low Reynolds number.
Source: https://dlatreyte.github.io/terminales-pc/chap-20/chap-20-2/chap-20-2-dynamique-fluides-6.png
As you noticed, both previous streamline patterns are practically the same despite both representing opposite conditions (Re→∞ and Re<<1) which is a clear inconsistency between the current interpretation of the theory and experiments. But, how should the streamline pattern be for a high Re condition? Is the CE a pure inertial manifestation? As we know from experiments around circular cylinders, as the Re increases, the flow separation point tends to move upstream, or in other words, to the top and bottom (+90 and -90 deg.) inviscid hypothetical separation points (see the next graph):
Fig. 4 Fluid separation angle vs Reynolds number for a circular cylinder.
In Fig. 4, it is clear that in the first limit condition (Re<<1; fully viscous), the separation angle tends to be located around 180 deg. (at the rear stagnation point; practically as in the previous experimental picture). On the other side, for the second limit condition (Re→∞) such a point (in fact, two points) tends to be located around +/-90 deg. (see Achenbach's results), which is completely compatible with a fully inviscid (or pure inertial!) assumption. Thus, how do we solve such a problem through a correct interpretation of the PFT? Well, I have a proposal based on the vortex lattice method (VLM) concepts [1]. What do you think? For sure, it should not be a steady but an unsteady solution by itself, including turbulent flow behind the body.
Fig. 5 Proposal to solve a true ideal flow past a circular cylinder.
Finally, it can be physically demonstrated that the CE can not be present in any inertial-dominated flow independently of the surface's curvature radius, as can be seen in the next two pictures, retrieved from 'An Album of Fluid Motion' (Van Dyke, 1982), in which water (even a viscous fluid!) flowing at high Re conditions (Re=2k and Re=10k, respectively) does not show any CE feature (the fluid does not 'laminarly' surrround the body at those Re conditions). Then, it can be concluded that, in a more strict and general sense, such an effect does not only depend on surface curvature or the existence of viscosity by itself, but on the relation between inertial and viscous forces (Re).
Fig. 6 Water past a circular cylinder at different Reynolds numbers.
I invite you to explore this blog and find more posts related to it! Thanks for sharing.
*Strictly speaking, the original Coanda effect is a phenomenon that occurs when a fluid jet perturbs its surroundings (velocity and pressure fields).
[1] Journal article: The Full Multi-wake Vortex Lattice Method: a detached flow model based on Potential Flow Theory | Advances in Aerodynamics | Full Text (springeropen.com)
Comments
Post a Comment